El teorema de Torricelli és un principi de mecànica de fluids que estudia el comportament d'un fluid en un recipient amb un forat. Per aquesta raó també se'l coneix com a principi de Torricelli.
El principi de Torricelli és utilitzat a la hidràulica i la fluidodinàmica per determinar la velocitat de flux d'un líquid a través d'un orifici. En general, la llei de Torricelli pot ser aplicada a diferents àrees, com l'enginyeria civil, la hidrologia, la física i la meteorologia, entre d'altres.
Aquest principi va ser enunciat pel físic i matemàtic italià Evangelista Torricelli al segle XVII.
Definició del teorema de Torricelli
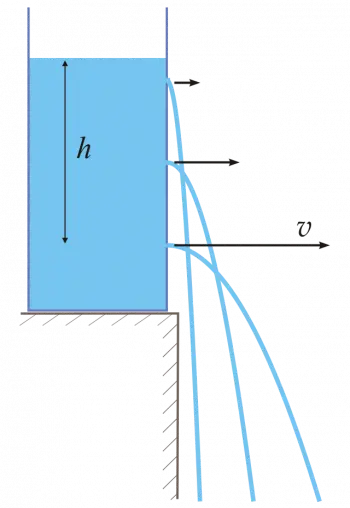
El principi de Torricelli estableix que la velocitat d'un líquid que flueix per l'orifici d'un recipient és igual a la velocitat que adquireix un cos que caigués lliurement des d'una altura igual a la distància des del nivell del líquid fins al centre de gravetat de l'orifici.
Les característiques del fluid perquè el teorema sigui vàlid és que el fluid ha de ser incompressible, amb viscositat nul·la i ha d'estar sotmès únicament per força gravitatòria.
Aquest teorema es basa en la llei de conservació de lenergia mecànica, que estableix que lenergia total dun sistema tancat es conserva. Concretament, és una conseqüència del principi de Bernouilli.
Equació de Torricelli
L'equació de Torricelli descriu la velocitat d'un fluid que flueix a través d'un orifici a causa de la diferència d'alçada entre el fluid al recipient i l'orifici de sortida. És una forma derivada de la llei de conservació de l'energia, i s'expressa de la manera següent:
\[
v = \sqrt{2gh}
\]
On:
- \( v \) és la velocitat de sortida del fluid (en metres per segon).
- \( g \) és l'acceleració deguda a la gravetat (aproximadament \( 9.81 \, \text{m/s}^2 \)).
- \( h \) és l'altura del fluid al recipient sobre el nivell de l'orifici de sortida (en metres).
Explicació:
- El principi de Torricelli estableix que la velocitat amb què un fluid abandona un recipient és equivalent a la velocitat que tindria un objecte que caigués lliurement des d'una altura h (a causa de l'acció de la gravetat).
- L'equació es basa en la conversió de l'energia potencial del fluid (a causa de la seva altura) en energia cinètica (a causa de la velocitat de sortida).
Aquesta equació és vàlida sota el supòsit que el flux és ideal, sense pèrdues per fricció o altres factors complicants.
Exemples del principi de Torricelli
El principi de Torricelli es pot observar en una gran varietat de situacions pràctiques. A continuació se'n presenten alguns exemples:
Tub de Pitot
El tub de Pitot és un instrument utilitzat per mesurar la velocitat de fluids, com l'aire en aeronaus o líquids en canonades.
Consisteix en dos tubs: un mesura la pressió estàtica (la pressió que el fluid exerceix uniformement), mentre que l'altre mesura la pressió total (que inclou la pressió dinàmica a causa del moviment del fluid). La diferència entre aquestes dues pressions es fa servir per calcular la velocitat del fluid, aplicant el principi de Torricelli. Aquest dispositiu s'utilitza en aeronàutica per conèixer la velocitat de l'avió i també es fa servir en enginyeria per avaluar el flux en sistemes hidràulics.
Fonts ornamentals i raigs d'aigua
Les fonts d'aigua, especialment les ornamentals, utilitzen el principi de Torricelli per generar raigs d'aigua a través d'un filtre.
La velocitat de l'aigua que emergeix de la font està directament relacionada amb l'alçada de l'aigua al dipòsit que l'alimenta. Com més gran sigui l'alçada de l'aigua, més gran serà la pressió a la base, cosa que incrementa la velocitat del flux a través del filtre.
Aquest principi s'utilitza no només en fonts decoratives, sinó també en sistemes de reg i en fenòmens naturals com els guèisers, on la pressió de l'aigua calenta empeny el líquid cap amunt.
Ompliment d'ampolles i recipients
Quan s'aboca un líquid des d'un recipient gran cap a una ampolla o un got, el flux de líquid es veu influenciat per la diferència d'alçada entre els nivells de líquid als dos recipients.
Inicialment, el flux és ràpid a causa de l'alta pressió generada pel líquid al recipient gran. No obstant això, a mesura que el nivell de líquid al recipient gran disminueix, la pressió es redueix, cosa que fa que el flux es torni més lent. Aquest comportament és explicable pel principi de Torricelli, que indica que la velocitat del fluid a l'orifici depèn de l'alçada de la columna de líquid.
Drenatge de dipòsits i tancs
El principi de Torricelli també s'aplica al drenatge de líquids de tancs o de dipòsits.
Quan un líquid flueix des d'un tanc mitjançant una vàlvula o un orifici a la part inferior, la velocitat amb què el líquid surt està determinada per la diferència d'alçada entre el nivell del líquid al tanc i la sortida. Com més gran sigui aquesta diferència d'alçada, més gran serà la velocitat del flux, cosa que permet buidar el tanc més ràpidament.
Aquest fenomen s'observa en sistemes com ara cisternes d'aigua, torres d'emmagatzematge i sistemes de drenatge.
Orificis en recipients perforats
Quan un recipient ple d'aigua té un orifici a la paret lateral, l'aigua comença a fluir cap a fora a causa de la pressió interna que exerceix el líquid al recipient. Segons el principi de Torricelli, la velocitat amb què l'aigua surt de l'orifici depèn de l'alçada del nivell d'aigua al recipient respecte a l'orifici.
A més altura, més gran serà la velocitat de l'aigua en sortir. Aquest fenomen es pot observar en experiments de física per il·lustrar com la pressió i la gravetat influeixen en el flux de líquids, i es dóna en situacions quotidianes com quan un recipient d'aigua té un petit forat al costat.
L'experiment de Torricelli
L'experiment de Torricelli, realitzat el 1643 pel físic i matemàtic Evangelista Torricelli, va demostrar l'existència de la pressió atmosfèrica i va ser clau per a la invenció del baròmetre.
Descripció de l'experiment
Torricelli va omplir un tub de vidre d'aproximadament un metre d'alçada amb mercuri i el va tapar amb el dit. Després, va invertir el tub i el va submergir en un recipient també ple de mercuri.
En retirar el dit, va observar que el nivell del mercuri al tub descendia, però no es buidava per complet, quedant aproximadament 76 cm d'alçada de mercuri dins del tub.
Conclusió
- Torricelli va deduir que el mercuri no queia completament perquè la pressió atmosfèrica empenyia el mercuri dins del recipient, equilibrant el seu pes dins del tub.
- A la part superior del tub va quedar un espai buit (anomenat "buit torricellià"), cosa que va ser una de les primeres proves experimentals del buit a la natura.
- Va determinar que la pressió de l'atmosfera es podia mesurar per l'alçada del mercuri al tub, establint la base del primer baròmetre.
Aquest experiment va permetre comprendre millor la pressió de l'aire i va asseure les bases per al desenvolupament de la meteorologia i la física de fluids.
Experiment pràctic amb una ampolla del principi de Torricelli
Tot seguit mostrem un experiment molt senzill per il·lustrar el funcionament del teorema de Torricelli que ens pot servir també per explicar el mètode científic. Aquest experiment es pot fer amb materials que es poden trobar a casa.
Materials:
- Una ampolla de plàstic buida
- Un clau o agulla esmolada
- Aigua
Instruccions:
- Omple l'ampolla de plàstic amb aigua fins a la meitat.
- Perfora un petit forat a prop de la meitat de l'ampolla amb el clau o l'agulla.
- Col·loqueu un recipient sota l'ampolla per recollir l'aigua que surt pel forat.
- Obre la tapa de l'ampolla per permetre que l'aire entri i l'aigua flueixi suaument.
Observacions:
Quan el forat es fa a l'ampolla, l'aigua comença a fluir a través del forat. La velocitat de l‟aigua disminueix a mesura que més aigua surt de l‟ampolla. Les partícules daigua que surten del forat descriuen la trajectòria típica dun tir parabòlic amb una velocitat inicial horitzontal.
Sabent l'alçada del forat respecte de la superfície del recipient on cau l'aigua i la distància horitzontal de l'aguger al punt on cau l'aigua, podem calcular la velocitat de sortida de l'aigua en qualsevol moment.