El moviment circular uniforme (MCU) és un concepte fonamental en cinemàtica que descriu un tipus específic de moviment on un objecte es desplaça al voltant d'un punt fix en una trajectòria circular a una velocitat constant.
En aquest article, definirem el MCU, i els diferents conceptes bàsics relacionats amb aquest moviment, alguns exemples reals que il·lustrin aquest moviment, les fórmules per calcular-lo i resoldrem alguns exercicis per comprendre'l millor.
Definició del moviment circular uniforme (MCU)
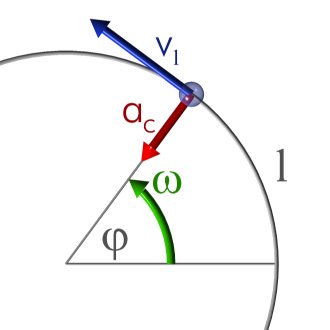El moviment circular uniforme (MCU) és un tipus específic de moviment on un objecte es desplaça al voltant d'un punt fix en una trajectòria circular a una velocitat constant.
Al MCU, la velocitat de l'objecte es manté invariable en magnitud i direcció al llarg del seu recorregut, cosa que significa que la velocitat angular és constant.
El moviment circular uniforme es caracteritza per la relació entre la velocitat angular i la velocitat lineal, que està directament relacionada amb el radi de la trajectòria circular.
Aquest moviment és típicament observat en situacions com l‟òrbita d‟un planeta al voltant d‟una estrella, el gir d‟una roda en un vehicle en moviment, o fins i tot en parcs d‟atraccions a les muntanyes russes, on els passatgers experimenten una sensació constant de velocitat i direcció a mesura que giren al voltant dun punt central.
Conceptes bàsics del MCU
Per comprendre el MCU, és fonamental familiaritzar-se amb alguns conceptes clau:
1. Període (T) i freqüència (f)
El període (T) és el temps que pren perquè l'objecte completi una volta completa al voltant de la trajectòria circular. La freqüència (f) és la quantitat de voltes que lobjecte completa en un segon. Estan relacionats de la següent manera:
f = 1 / T
Al Sistema Internacional d'Unitats (SI), el període es mesura en segons (s). Per altra banda, la freqüència es mesura en hertz (Hz). Un hertz és igual a un cicle per segon.
2. Velocitat angular (ω)
La velocitat angular (ω) és una mesura de la rapidesa amb què l'objecte es desplaça al voltant de la trajectòria circular. Es mesura en radians per segon (rad/s) i està relacionada amb la freqüència (f) de la manera següent:
ω = 2·π·f
3. Ràdio de la trajectòria (r)
El radi de la trajectòria (r) és la distància des del punt central a fi que es mou al MCU. Aquest valor és constant durant tot el moviment.
4. Velocitat lineal (v)
La velocitat lineal (v) és la rapidesa amb què l'objecte es mou tangencialment al llarg de la trajectòria circular. Per aquesta raó també es coneix com a velocitat tangencial.
La velocitat tangencial està relacionada amb la velocitat angular (ω) i el radi (r) de la manera següent:
v = r·ω
5. Acceleració centrípeta (ac)
L'acceleració centrípeta (ac) és una acceleració fictícia que actua sobre l'objecte en direcció oposada al centre de la trajectòria circular. La seva magnitud està relacionada amb la velocitat angular (ω) i el radi (r) de la manera següent:
a c =r·ω 2
Les unitats de l'acceleració centrípeta són metres per segon al quadrat (m/s²).
Fórmules del moviment circular uniforme
Les fórmules següents són essencials per comprendre i resoldre problemes relacionats amb el MCU:
-
Relació entre la velocitat angular i la velocitat lineal: v=rω
-
Relació entre el període i la freqüència: T=1/f
-
Relació entre la velocitat angular i la freqüència: ω=2πf
-
Relació entre l'acceleració centrípeta, la velocitat angular i el radi: a c =rω2
Exemples a la vida quotidiana
El moviment circular uniforme es troba en nombrosos aspectes de la vida quotidiana.
-
Turbines de vapor a centrals nuclears: Les turbines de vapor a centrals nuclears empren el MCU per convertir l'energia tèrmica en energia mecànica, generant electricitat.
-
Ventiladors de sostre: Les aspes dels ventiladors de sostre fan un MCU per circular l'aire de manera uniforme en una habitació, proporcionant refredament.
-
Els vehicles en corbes: els vehicles, en girar en corbes circulars, segueixen un MCU que es pot calcular fent servir aquestes fórmules.
-
Fabricació de cordes: Girar una corda per crear una soga implica un MCU, on la corda s'enrotlla de manera uniforme al voltant d'un nucli central.
Exercicis resolts
Ara, resolguem alguns exercicis típics relacionats amb el MCU:
Exercici 1
Suposem que un cotxe de carreres es desplaça a una velocitat constant de 100 m/s al voltant d´una pista circular de ràdio 200 metres. Calcula el període, la freqüència i la velocitat angular del moviment.
Solució:
Atès que la velocitat és constant, podem utilitzar la fórmula per a la velocitat angular:
v = r·ω
Substituint els valors coneguts:
100 m/s = 200 m ⋅ ω
Per trobar ω:
ω = (100 m/s) / 200 m=0.5 rad/s
Ara, podem trobar el període (T) utilitzant la relació entre la velocitat angular i la freqüència:
ω = 2·π·f
0.5 rad/s = 2·π⋅f
Per trobar f:
f = (0.5 rad/s) / (2·π) ≈ 0.0796 Hz
I, finalment, el període (T) és el recíproc de la freqüència:
T = 1/f ≈ 12.57 s
Exercici 2
Un objecte es desplaça durant una trajectòria circular de radi 4 metres a una velocitat angular de 2 radians per segon. Calcula'n la velocitat lineal i l'acceleració centrípeta.
Solució:
Per trobar la velocitat lineal, utilitzem la fórmula:
v = r·ω
Substituint els valors coneguts:
v=4m ⋅ 2 rad/s = 8 m/s
Per a l'acceleració centrípeta, fem servir la fórmula:
ac = r·ω2
Substituint els valors coneguts:
ac =4 m⋅(2 rad/s)2=16 m/s2
