El moviment circular uniformement accelerat (MCUA) és un tipus de moviment on un objecte es mou al llarg d'una trajectòria circular amb una acceleració constant.
El MCUA és un tipus de moviment crucial pel que fa al càlcul de la cinemàtica d'un cos. Aquest fenomen és fonamental per comprendre una àmplia gamma de situacions, des de la mecànica de vehicles fins a la dinàmica dels planetes en òrbita, i es pot descriure mitjançant fórmules específiques que relacionen la velocitat angular, lacceleració angular i el temps.
Què és el moviment circular uniformement accelerat?
El moviment circular uniformement accelerat (MCUA) és un concepte fonamental en la física que descriu el moviment d‟un objecte al llarg d‟una trajectòria circular amb una acceleració constant.
A diferència del moviment rectilini, en què un objecte es mou en línia recta, el MCUA involucra una variació constant en la velocitat angular de l'objecte, cosa que el porta a rotar al llarg d'una corba tancada.
A l'MCUA, l'acceleració angular de l'objecte és constant, cosa que significa que la seva velocitat angular augmenta o disminueix de manera uniforme amb el temps.
Característiques bàsiques del moviment
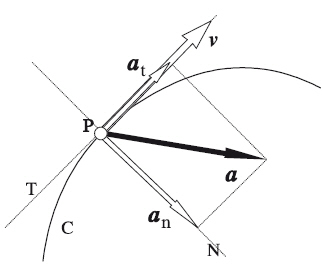Les característiques bàsiques que defineixen aquest moviment són:
- L'objecte es mou descrivint una trajectòria circular. Això implica laparició duna acceleració centrípeta per mantenir constant la distància de lobjecte al centre de rotació.
- La velocitat angular pateix una acceleració angular constant, per tant, la velocitat tangencial també pateix una acceleració tangencial.
Conceptes bàsics
Velocitat angular
La velocitat angular, representada per la lletra grega "ω" (omega), és una mesura de la rapidesa amb què un objecte gira al llarg de la trajectòria circular. Es mesura en radians per segon (rad/s).
Velocitat tangencial
La velocitat tangencial és la velocitat lineal d‟un objecte en un punt específic de la seva trajectòria circular. Es refereix a la magnitud de la velocitat d'un objecte en una direcció tangent a la corba en aquest punt.
Acceleració angular
L'acceleració angular, representada per "α" (alfa), és el canvi en la velocitat angular per unitat de temps. Igual que la velocitat angular, es mesura en radians per segon al quadrat (rad/s²).
Acceleració centrípeta
L´acceleració centrípeta és una acceleració dirigida cap al centre d´una trajectòria circular. Es produeix quan un objecte es desplaça en una òrbita corba i experimenta un canvi constant en la direcció de la velocitat sense afectar-ne la magnitud.
Acceleració tangencial
L‟acceleració tangencial és una mesura de com canvia la magnitud de la velocitat d‟un objecte en moviment al llarg d‟una trajectòria corba. Aquesta acceleració es produeix quan la velocitat tangencial de lobjecte varia.
Fórmules de càlcul
Fórmula de la velocitat angular en funció del temps
La relació entre la velocitat angular inicial (ω₀), l'acceleració angular (α) i el temps (t) es pot descriure mitjançant la fórmula següent:
ω= ω₀ + α·t
On
- ω és la velocitat angular final.
- ω₀ és la velocitat angular inicial.
- α és l'acceleració angular.
- t és el temps
Fórmula de l'angle rotat
La quantitat d'angle rotat (θ) en un temps "t" està relacionada amb la velocitat angular i l'acceleració angular de la manera següent:
θ = ω₀·t + ½·α·t²
On
- θ és l'angle rotat.
- ω₀ és la velocitat angular inicial.
- α és l'acceleració angular.
- t és el temps
Fórmula de la velocitat angular en funció de la velocitat angular
La velocitat angular final (ω) es relaciona amb la velocitat angular inicial, l'acceleració angular i l'angle rotat mitjançant la fórmula següent:
ω² = ω₀² + 2·α·θ
On
- ω és la velocitat angular final.
- θ és l'angle rotat.
- ω₀ és la velocitat angular inicial.
- α és l'acceleració angular
Exemples quotidians il·lustratius
El moviment circular uniformement accelerat (MCUA) es troba en nombrosos aspectes de la vida quotidiana i en diversos contextos, alguns exemples inclouen:
- Rentadora de roba: Al cicle de centrifugat, la roba gira al tambor amb una acceleració constant, permetent que l'aigua s'expulsi cap a fora.
- Jocs de fira: Les atraccions de fira, com les sínies i els carrusels, apliquen un MCUA per arrencar i parar per permetre que els passatgers puguin pujar i baixar.
- Aerogeneradors: els molins de vent pateixen un MCUA quan es posen en marxa o quan hi ha variacions a la intensitat del vent.
- Turbines de vapor: les turbines de central nuclear estan optimitzades per girar a una velocitat constant. Mentre es produeix el moviment circular uniformement accelerat durant l'arrencada i l'atur, la seva eficiència és més baixa.
Exercicis resolts
Exercici 1: Rotació d'un ventilador
Un ventilador gira amb una velocitat angular inicial de 3 rad/si experimenta una acceleració angular de 0.5 rad/s². Quant de temps us portarà assolir una velocitat angular de 7 rad/s?
Solució
Utilitzem la fórmula per a la velocitat angular final:
ω = ω₀ + αt
Substituïm els valors coneguts:
7 rad/s = 3 rad/s + (0.5 rad/s²)·t
Resolem per a t:
(0.5 rad/s²)t = 7rad/s − 3 rad/s
0.5t = 4 rad/s
t=(4 rad/s) / (0.5 rad/s²) = 8 s
El ventilador prendrà 8 s per assolir una velocitat angular de 7 rad/s.
Exercici 2: Gir d'una sínia
Una sínia comença a girar des del repòs amb una acceleració angular de 0.8 rad/s². Quant de temps prendrà perquè la sínia giri 5 radians?
Solució
Utilitzem la fórmula per a l'angle rotat:
θ = ω₀t + ½·α·t²
Substituïm els valors coneguts:
5rad = (0 rad/s)·t + ½(0.8 rad/s²)·t²
Simplifiquem l'equació:
5rad = (0.4 rad/s²)t²
Resolem per a t:
t = √( 5 rad / 0.4 rad/s²)
t ≈ 3.54s
La sínia prendrà aproximadament 3.54s per girar 5 radians des del repòs.