La Llei de la Gravitació Universal de Newton és un dels pilars fonamentals de la física i va ser desenvolupada per Sir Isaac Newton al segle XVII. Aquesta llei descriu la força d'atracció entre dos cossos a causa de la massa i la distància relativa.
És una de les lleis més importants i àmpliament aplicades al camp de la física clàssica i ha permès comprendre i predir molts fenòmens a l'univers.
En aquest article, explorarem detalladament què és la Llei de la Gravitació Universal, la seva fórmula, la seva importància i alguns exemples que il·lustren la seva aplicació.
Què és la Llei de la Gravitació Universal?
La Llei de la Gravitació Universal estableix que la força d'atracció entre dos cossos és directament proporcional al producte de les masses i inversament proporcional al quadrat de la distància que els separa.
És a dir, com més gran sigui la massa dels objectes i més a prop estiguin entre si, més gran serà la força d'atracció gravitacional entre ells.
La fórmula de la Llei de la Gravitació Universal:
La fórmula matemàtica per calcular la força gravitacional entre dos objectes s'expressa de la manera següent:
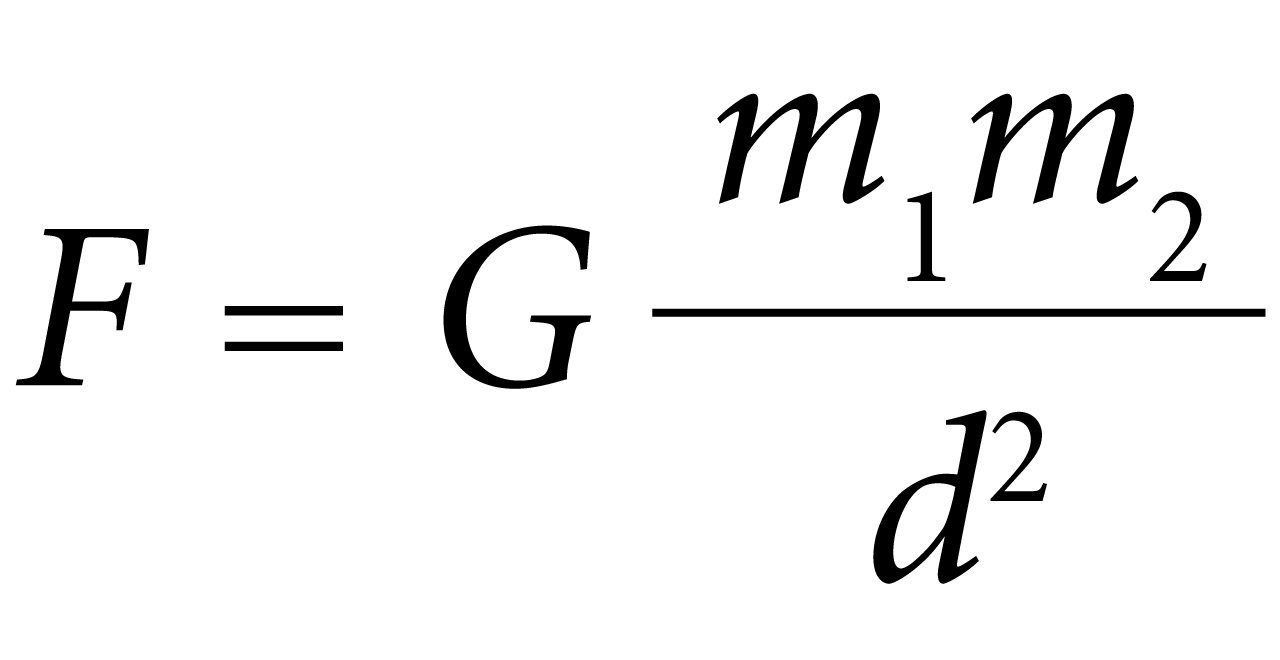
On:
-
F és la força gravitacional entre els objectes expressada en newtons,
-
G és la constant de gravitació universal, aproximadament 6.674 × 10-11 N (m/kg)2
-
m 1 im 2 són les masses dels objectes expressada en quilograms (kg).
-
r és la distància entre els centres de massa dels objectes expressada en metres (m).
La constant de gravitació universal (G) té un valor de 6.674 × 10-11 N (m/kg)2 aproximadament i s'utilitza per escalar la força d'atracció en funció de les unitats de massa i distància utilitzades.
Importància de la Llei de la Gravitació Universal:
La Llei de la Gravitació Universal és molt important en l'estudi i la comprensió de l'univers. A través d'aquesta llei, podem explicar i predir fenòmens com l'òrbita dels planetes al voltant del Sol, els moviments de les llunes al voltant dels planetes i la interacció entre objectes massius a l'espai.
A més, la llei també té aplicacions pràctiques a la vida quotidiana. Per exemple, permet entendre el funcionament dels satèl·lits artificials que orbiten al voltant de la Terra i és essencial per a la navegació espacial i la planificació de missions espacials.
Exemples de l'aplicació de la Llei de la Gravitació Universal:
A continuació mostrem 4 exemples en què s'aplica la llei de la gravitació universal de Newton:
1. Òrbita de la Terra al voltant del Sol
La força gravitacional entre la Terra i el Sol és responsable de mantenir el nostre planeta en una òrbita estable al voltant de l'estrella.
Aquesta força permet que la Terra es mantingui en moviment circular al voltant del Sol i en determina el període d'un any. La força que exerceix el Sol sobre la Terra és perpendicular a la velocitat lineal de la Terra a cada moment.
2. La Lluna i les marees
La força gravitacional entre la Terra i la Lluna és la responsable de les marees. La Lluna exerceix una força d'atracció sobre els oceans, cosa que provoca l'ascens i el descens del nivell de l'aigua a mesura que la Terra trencada.
Igual que passa amb el Sol i la Terra, aquesta força és la força centrípeta que obliga la Lluna a orbitar al voltant de la Terra.
3. Satèl·lits artificials
En el disseny i funcionament dels satèl·lits artificials també es fan càlcules utilitzant la fòmrula de la llei de la gravitació universal.
Per mantenir un satèl·lit en òrbita, cal una velocitat i altitud específiques que equilibrin la força gravitacional amb la força centrífuga generada pel moviment orbital.
4. Caiguda dobjectes
La llei també s'aplica a la caiguda d'objectes a la superfície de la Terra. Com més gran sigui la massa de l'objecte, més gran serà la força gravitacional que actua sobre ell i més ràpid caurà.
Exercicis de la llei de la gravitació universal
Tot seguit mostrem tres exercicis resolts que il·lustren l'aplicació d'aquesta llei de la física:
Exercici 1: Calculant la força gravitacional entre dos cossos
Suposem que tenim dos objectes: un amb una massa de 5 kg i un altre amb una massa de 8 kg. La distància entre els centres de massa dels objectes és de 2 metres. Volem calcular la força gravitacional entre ells.
Dades
-
m1 = 5 kg
-
m2 = 8 kg
-
r = 2 m
-
G = 6.674 × 10-11 N (m/kg)2
Solució:
Utilitzem la fórmula de la Llei de la Gravitació Universal:
F = G (m1 ·m2 ) / r2
Substituint els valors coneguts:
F = (6.674 × 10-11 N (m/kg)2 ) * (5 kg * 8 kg) / (2 m)2
F = 6,674 × 10-10 N
Per tant, la força gravitacional entre els dos cossos és aproximadament de 6,674×10 -10 N.
Exercici 2: Calculant la força gravitacional entre la Terra i un objecte
Suposem que volem calcular la força gravitacional entre la Terra (massa ≈ 5.972 × 1024 kg) i un objecte amb una massa de 100 kg. La distància entre el centre de la Terra i l'objecte és de 6.371 × 106 metres (ràdio aproximat de la Terra).
Dades:
-
m 1 (massa de la Terra) = 5.972 × 1024 kg
-
m 2 (massa de l'objecte) = 100 kg
-
r (distància) = 6.371 × 106 m
-
G = 6.674 × 10-11 N (m/kg) 2
Solució:
Apliquem la fórmula de la Llei de la Gravitació Universal:
F = G (m1 ·m2 ) / r2
Substituint els valors coneguts:
F = (6.674 × 10-11 N (m/kg) 2 ) * ((5.972 × 1024 kg) * (100 kg)) / (6.371 × 106 m)2
F = 981.95 N
Per tant, la força gravitacional entre la Terra i lobjecte és daproximadament 981.95 N.
Exercici 3: Calculeu la massa d'un objecte a partir de la força gravitacional
Suposem que tenim dos objectes, i sabem que la força gravitacional és de 100 N. La distància entre els objectes és de 10 metres i la massa d'un dels objectes és de 5 kg. Volem calcular la massa del segon objecte.
Dades:
-
F = 100 N
-
r = 10 m
-
m1 = 5 kg
-
G = 6.674 × 10-11 N (m/kg)2
Solució:
Fem servir la fórmula de la Llei de la Gravitació Universal i aclarim m2:
F = G (m1 ·m2 ) / r2
Aclarim m2:
m2 = (F * r2 ) / (G * m1 )
Substituint els valors coneguts:
m 2 = (100 N * (10 m)2 ) / ((6.674 × 10-11 N (m/kg)2 ) * 5 kg)
m 2 ≈ 2.997 × 1013 kg
Per tant, la massa del segon objecte és aproximadament de 2997 × 1013 kg.
